It is not every day that one encounters a question left unanswered by Google, especially when it’s very specific and related to programming. So, to ruin this one for everyone else, here’s my solution to a cute little coding riddle from a classic old game.

Background

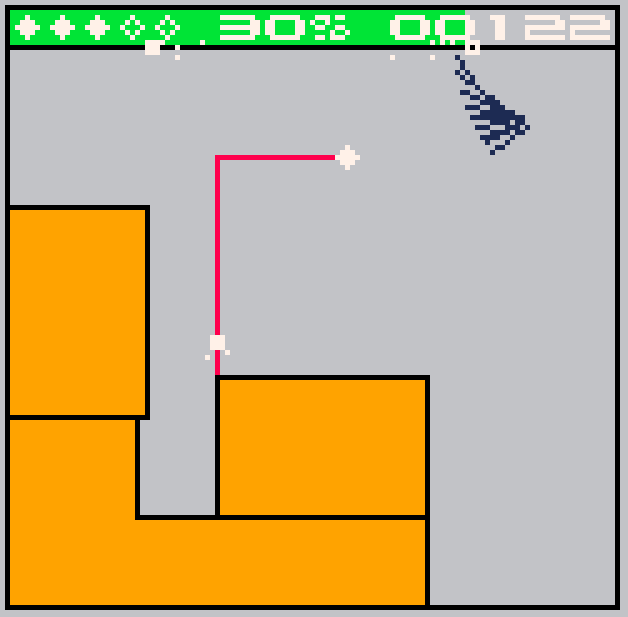
My first encounter with Qix, or rather a Qix clone, happened when I was about twelve years old, on a cousin’s PC that had a green monochrome monitor. It wasn’t much in terms of graphics, or sound, or anything really: far less impressive, in fact, than the original, 1981 arcade version you can see on Youtube. If memory serves, instead of the colorful, deadly animated line which is the true Qix, the game I saw only had a small square bouncing around.

Nonetheless, it presented a compelling challenge. With your own little square you had to draw continuous lines, like a keyboard-operated etch-a-sketch; if the Qix hit your line, or the line hit itself, you died. However, if you managed to draw all the way back to an existing area (the play field frame or something you drew earlier), the new area was filled solid and became inaccessible to the Qix. When a large enough percentage of the play field was filled, you won the level. This required both fast reflexes and planning, both audacity and patience.

Which Side to Fill

As a typical twelve-year-old, I enjoyed the game without pondering about its inner workings. I drew outlines, the game filled inside them, the Qix continued to threaten on the outside. That’s just how it was. Only years later, when I started programming little games on my own, it suddenly hit me: How did the game know what “side” of the outline to fill? For an extreme example, if I manage to draw a straight line that splits the play field in half, what makes the game fill one half and not the other?

Obviously, it wasn’t a random call. By some mysterious process, the Qix never got painted over. It was always the other area that got filled. But, given that the newly drawn outline can form a very complex polygon spanning all over the place, how can the computer tell? And, perhaps just as important, how could the computer do this, almost in real time, back when its processing power was laughable relative to modern machines?

Less Likely Solutions

A disclaimer is in order here: I have no inside information. I don’t really know how the original Qix, or any of its commercial clones, worked. Perhaps everything I write from here on is wrong. But if it is, to paraphrase Einstein, then I would feel sorry for the programmers. Also, the fact that I couldn’t find an authoritative solution on the web doesn’t mean it’s not there – maybe it was just hiding from me really well.

The first solution that turned up, which was even implemented on a modern clone on GitHub, goes like this: “The computer fills the smaller area”. While at the bottom line this is usually true (since it’s extremely hard to draw big outlines with the erratic Qix around), it still feels like wishful thinking rather than a solid, always-correct algorithm. To make things worse, how would the computer even know which area is the smaller one? How would it measure?

It’s a bit like asking about a shoot ’em up game, “How does the enemy spaceship know where to fire”, and getting the answer “it fires at the player”. Well yeah, but how does the algorithm actually work out the angles? The implementation I saw used a little spatial inference to get two points, one inside the newly-drawn polygon and the other one outside it; then it ran a mock flood-fill algorithm from each, counting the pixels*, then did an actual flood-fill with the one that turned out smaller. While old computers had low screen resolutions, and therefore could do flood-fills relatively fast, I still find this solution convoluted and risky. Next, please!

* It should be noted that the minimal “screen unit” of a game can be a square larger than a single actual pixel. But the principle still holds.

A variant of the above solution goes like this: get an inside and an outside point, simulate a flood-fill from one of them. If this mock fill touches the Qix, then we’re on the wrong side; start the actual fill from the other point. However, if the mock fill is finished without touching the Qix, perfect – now just do the same fill for real. This algorithm is better than the previous because it can’t make a mistake. But it requires a lot of checking, and that would strain older systems.

A wholly different approach suggests recording the player’s drawing in real time, turn by turn and line by line, as an actual polygon. When it’s completed, we can test whether the Qix is inside it or not (“is a point inside a polygon?” – a classic spatial puzzle), then fillPoly or flood-fill the appropriate area. This seems legit at first glance, but gets really nasty when we get down to the details. After all, the points where the player started and finished the outline can be essentially anywhere, and we’ll need a complex algorithm just to figure out how to close the gap correctly.

Then there was the idea to start from the Qix and move in a straight line until we hit a filled area (or the frame), then trace around until we get back to the same point. The area thus outlined should stay as it is; again, not too trivial, and it was not explained how we are supposed to find the other area to fill.

My Solution

Actually, I developed my own solution before I ever looked up any other. Not because I’m such a clever frood, but simply because, for a long time, I couldn’t recall the name of the game. Anyway, I rejected upfront any geometry-related solution. Too complicated. That leaves flood-fill. As mentioned above, this action doesn’t have to happen on-screen: it can be “simulated” on an off-screen buffer, for example. The key point is that we don’t have to fill with the same value in all circumstances.

Following from that idea, when we detect that the player has finished an outline, we go to the Qix (or any point thereof), and flood-fill from it with a special “color” we’ll call “Qix-area”. When finished, we simply iterate over all the pixels on the screen, replacing every “Empty” with “Filled” and every “Qix-area” with “Empty”. That’s it! No deducing points, no counting. If we’re clever enough with the color palette, even the pixel replacement can be speeded up.

It should be remembered that flood-fill itself, at least the textbook version, is resource-intensive. Going over all the pixels is also not trivial in terms of processing speed. However (again, especially given the low screen resolutions of the old days), there are plenty of tricks and optimizations we can do to streamline both tasks. Maybe we’ll discuss these some other time.

Of all the solutions I know of to the Qix fill problem, mine appears to be the simplest and fastest in terms of computation and data representation, and lenient on RAM too. That is why I believe the same algorithm was used back in the eighties, when programmers didn’t have much choice anyway.

If you have a better idea, or better information than I could find, please do share in the comments!