אתגר תכנות קטן ישמש לנו קרש קפיצה לדיון על הגדרות, ספציפיות והכללה, ייצוגי מידע ומה לא.

בבלוג "מאיה כותבת אלגוריתמים", שמצאתי לא מזמן במקרה, הכותבת עושה את מה שאני מנסה לעשות כבר שנים ולא מספיק: למצוא חידות ואתגרי תכנות ולנסות לפתור אותם. אחד מהאתגרים שעלו שם הוא זה:

"צריך לכתוב 4 פונקציות שונות שמקבלות מספר אחד – 5 או 7 ומחזירות את המספר השני. הפונקציות צריכות להיות שונות אחת מהשנייה במהותן ואסור להן להשתמש בשום סוג של if,switch וכיוצ"ב."

אתם מוזמנים לעצור כאן ולחזור אחרי שתחשבו על זה לבד, כי אני מתכוון להציג בהמשך כמה פתרונות.

מה השאלה?

לפני הפתרונות השגרתיים והוויכוחים עליהם, הסתכלו על קוד פייתון הבא (בחרתי לעבוד בפייתון למען הנוחות, כמובן שיש הבדלים מסוימים במה שאפשר או אי אפשר לעשות בכל שפה):

def myFunc(x):
    while (5 == x):
        return 7
    return 5

זה עובד, אבל האם זה עומד בדרישות החידה? אין כאן שום if או תנאי מוצהר אחר, ועם זאת אנחנו יודעים שהמימוש של while (או לצורך העניין, כל לולאה אחרת) על ידי הקומפיילר/אינטרפרטר כן מבצע בסופו של דבר בדיקה מפורשת של תנאי הלולאה. זו נקודה חשובה, כי אם נסרב לקבל פתרונות שיש בהם תנאי כלשהו – כל הדרך עד לאסמבלי, כולל – הרבה מאוד אפשרויות ייפסלו.

גם הדרישה הבאה של החידה לא מובנת מאליה. שהפונקציות יהיו שונות במהותן – מה בעצם זה אומר? ניקח פתרון קלאסי מבוסס-חשבון:

return 12 - x

ועוד אחד:

return 35 / x

וניקח פתרון שלישי, קצת פחות מובן מאליו אבל עדיין מבוסס חשבון:

return 9 - int(x*x/10)

האם שלוש הדרכים האלה "שונות אחת מהשנייה במהותן"? אם נחליט שהמהות של כל הפתרונות לעיל היא "תרגיל חשבוני", וזו החלטה סבירה בהחלט, אז כולם כמובן שקולים וייחשבו, מבחינת המהות, רק פונקציה אחת. אם כך, מה דינו של הפתרון הבא?

return eval('12' + '-1'*x)

הוא אמנם ניגש לבעיה בדרך עקיפה מאוד, אך בסופו של דבר אנחנו מבינים שהוא עושה בדיוק את מה שכבר ראינו קודם, קרי חישוב שתים-עשרה פחות x. נחשב או לא נחשב? ומה עם דרכים חשבוניות עוד יותר מתפתלות, כמו זו?

import datetime

def myFunc(x):
    return datetime.date(2019, x, 26).weekday()+1

הופעה ייצוגית

נניח שכל הפתרונות החשבוניים שקולים ומהווים רק תשובה אחת מתוך הארבע הדרושות. מה עוד נשאר? אנחנו יכולים, למשל, לא להסתמך ישירות על הערך המספרי שקיבלנו, אלא על הייצוג שלו בזיכרון המחשב. כך,

return x ^ 2

זוהי תשובה שאין בה שום פעולה חשבונית, לא מפורשת ולא סמויה, ושום תנאי – רק מניפולציית ביטים פשוטה, היפוך הביט השני מימין בייצוג הבינארי של המספר (חמש בבינארי הוא 101 ושבע הוא 111). לדעתי זה שונה מהותית מהפתרונות הקודמים. אמנם הייצוג הבינארי עצמו יכול להיחשב פעולה חשבונית, אבל אנחנו לא צריכים אותו. את אותו הדבר אפשר לעשות עם הייצוג הבינארי של התווים "5" ו-"7" בקוד ASCII, שהוא מוסכמה בלבד, ומן הסתם גם בהרבה ייצוגים אחרים.

אתם יודעים מה, בואו נתפרע קצת עם הקטע הזה של ייצוגים. חישבו למשל על תצוגת 7 מקטעים קלאסית שכל מייקר מכיר. אם נוכל להציג את המספר x על גבי תצוגה כזו, ובדרך כלשהי לספור כמה מקטעים מוארים בה, ולהוסיף 2 לסכום, נקבל את התשובה הנכונה!

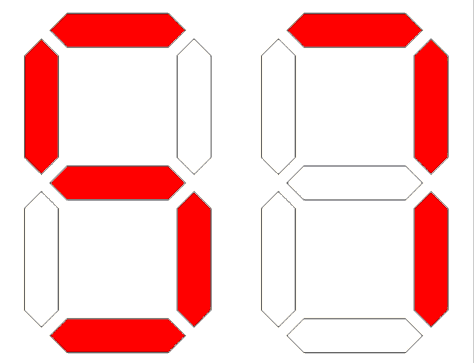
אפילו יותר מאשר בקוד ASCII, הייצוג הגרפי הזה של 5 ו-7 הוא מוסכמה שרירותית לחלוטין, ועדיין אפשר לעשות עליה מניפולציות ולהגיע לתשובות הרצויות.

הטבלה לא משקרת

סוג הפתרון המהותי השלישי הוא שוב להשתמש בערך של x, אבל הפעם לא כמרכיב חשבוני בתשובה, אלא פשוט כרפרנס (אינדקס, מצביע, פוינטר…) לטבלת חיפוש כזו או אחרת. זה יכול להיראות כך:

LUT = (0, 0, 0, 0, 0, 7, 0, 5)
return LUT[x]

או משהו עקום כמו זה:

def my5Func():
    return 7

def my7Func():
    return 5

def myFunc(x):
    return eval("my" + str(x) + "Func()")

בתגובה שכתבתי בבלוג של מאיה הצעתי עוד רעיון: לקחת מערך בגודל 7 תאים שבכולם כתוב 7, לכתוב את הערך "5" ל-x התאים הראשונים, ולהחזיר את הערך שבתא האחרון. בקוד זה נראה ככה:

def myFunc(x):
    a = [7]*7
    for n in range(x):
        a[n] = 5
    return a[6]

יש לנו כאן לולאות, אך עם קצת מחשבה אפשר להיפטר מהן ולהשיג את אותה מטרה בדיוק:

def myFunc(x):
    a = [7, 7, 7, 7, 7, 7, 7]
    a[x - 1] = 5
    return a[6] 

זו לא טבלת חיפוש סטנדרטית, ואף על פי כן השימוש ב-x בקטע הקוד הזה הוא כרפרנס.

עמוק לתוך החומרה

כמה אנשים הציעו פתרון מעניין, שלכאורה לא נופל לאף אחת מהקטגוריות הקודמות. הנה הגרסה שלי:

def myFunc(x):
     try:
         return 10 / (x - 5)
     except:
         return 7

מזכיר במובן מסוים את הפתרון הראשון שהצעתי בפוסט זה, אך במקום להסתמך על התנאי המובלע של הלולאה, כאן השגיאה של חלוקה באפס קופצת, כביכול, כבר ברמת החומרה. כמו פסיקה (interrupt) במיקרו-בקר, שאינה תלויה כלל בקוד שלנו.

האם זה באמת כך? היכן ואיך בדיוק מתבצעת הלכידה של חלוקה באפס? זה תלוי מן הסתם בשפת התכנות, בקומפיילר, במערכת ההפעלה ובמעבד. אין לי מספיק ידע כדי להיכנס לקרביים של האינטרפרטר של פייתון ולהבין מה קורה שם; אני מוכן לקבל שבמקרים בהם הפעולה הלא-חוקית נתפסת בתוך ה-CPU, פתרון שכזה עדיין מקיים את תנאי החידה.

שיטה חמישית?

בנקודה זו נתקעתי. בהכללה, נמצאו ארבע שיטות עקרוניות שונות לפתור את השאלה, שלא מכילות בתוכן תנאים סמויים (לפחות עד רמת האסמבלי): פעולה חשבונית, מניפולציה על ייצוג, שימוש בערך כרפרנס, והסתמכות על שגיאות ברמת ה-CPU. כל הפתרונות הנוספים שחשבתי עליהם בינתיים, או ראיתי שאחרים הציעו, היו מבוססים על אחת או יותר מבין ארבע השיטות הנ"ל, או הסתמכו על תנאים סמויים. השאלה הגדולה באמת כעת היא: האם יש שיטה עקרונית נוספת?