בעיית תכנות קלאסית בתחום הגרפיקה, שפתרונה מסתמך בדרך כלל על רקורסיה או מחסנית (Stack), מקבלת טוויסט מעניין כשצריך לממש אותה על מיקרו-בקר עם מגבלות זיכרון חריפות.

מילוי שטחים: מה הבעיה?
למי שאינו מתחום המחשבים, המחשה טובה לנושא של מילוי שטחים היא חוברת צביעה לילדים: יש שטחים מוגדרים, בצורות שונות ומשונות אבל סגורים בתוך קווים ברורים, והמשימה היא למלא אותם לגמרי בצבע בלי לחרוג מהגבולות. לבני האדם זוהי משימה קלה מאוד – אפילו לילדים קטנים האתגר הוא כמעט תמיד מוטורי בלבד – אך כשמחשב צריך לעשות זאת ולשנות צבע של אזור בתמונה, זה לא מובן מאליו.
יש הרבה גישות ושיטות למילוי שטחים ממוחשב, והן תלויות קודם כל בייצוג המידע. למשל, האם הקווים שתוחמים את השטח מוגדרים כווקטורים מתמטיים ממש, או שקיים מערך דו-ממדי של פיקסלים שמייצג תמונה? במקרה של פיקסלים, אחת השיטות המפורסמות היא Flood Fill: אנחנו שופכים, כביכול, עוד ועוד צבע לנקודת ההתחלה ונותנים לו להציף ולהתפשט לכל עבר, עד שהוא מגיע לפיקסלים בצבע שונה – מחסומים – שאותם קבענו שהוא לא יכול לעבור.
אך כמובן שבזיכרון המחשב הצבעים והפיקסלים הם רק מספרים, ובניגוד לבני האדם, הקוד אינו תופס את התמונה הכוללת: הוא אינו יכול "לראות מעבר לפינה" ולתכנן את הצביעה, ולמעשה הוא מסוגל לבדוק ולשנות אך ורק פיקסל אחד כל פעם. כאן מתגלה כוחו של פתרון רקורסיבי: אנחנו לוקחים פיקסל מסוים, ואם הוא ריק אז א) משנים לו את הצבע, ו-ב) עושים את אותו הדבר בדיוק עם כל אחד מארבעת הפיקסלים השכנים (מעליו, מתחתיו, מימינו ומשמאלו). קלאסי! נוסיף עוד כמה פרטים קטנים, כגון גבולות התמונה ומיקום הפיקסל הריק ההתחלתי, והפונקציה הקטנה והפשוטה הזו תעבוד היטב.
היטב – אבל לאט ובצורה בזבזנית, כי כידוע, כל קריאה לפונקציה טומנת בחובה פעולות והקצאת זיכרון מאחורי הקלעים, וכשיש לנו תמונה עם הרבה פיקסלים, זה אומר המון קריאות רקורסיביות. כדי להתמודד עם הקושי הזה אפשר לעשות כל מיני דברים, כגון מילוי אופקי של יותר מפיקסל יחיד בכל ריצה של הפונקציה, או אחסון המידע על מקומות שעוד צריך לבדוק במחסנית אחת מסודרת, במקום שיסתתר בין כל הקריאות. אבל גם מחסנית תופסת מקום בזיכרון, וכידוע לכם בעולם האמבדד – במיוחד במיקרו-בקרים פשוטים כמו של ארדואינו אונו – לעתים קרובות הזיכרון הוא המשאב המוגבל ביותר.
רגע… מה הקשר של ארדואינו לתמונות עתירות פיקסלים? ובכן, הקשר הוא באמת קצת רופף, אך לא לגמרי מופרך, ואני מקווה שאוכל לחזור בקרוב לפרויקט שהזנחתי ולתת לכם דוגמה מצוינת. בינתיים, תאמינו לי שיכולים להיות מצבים שבהם נצטרך לבצע Flood Fill כלשהו בעזרת מיקרו-בקר פשוט, ורקורסיה או מחסנית לא יהוו אופציה.
הדגמות ברקורסיה
על מנת שכל הדיבורים האלה לא יהיו באוויר, כתבתי במחשב תוכנה שמממשת Flood Fill בשני אופנים רקורסיביים, ומודדת את מספר הקריאות לכל פונקציה רקורסיבית ואת העומק המרבי שהיא מגיעה אליו. במקום תמונה של ממש נתתי לתוכנה מערך של מחרוזות, שמייצג מין תמונה ברזולוציה נמוכה של 80×25, כמו מסכי הטקסט של פעם. התמונה הזו יכולה להיות כל דבר, החל ממסגרת מלבנית פשוטה (ראו בצילום המסך הבא) ועד למבוך שיאתגר את האלגוריתם ויעזור באיתור באגים בעת הצורך. למען הפשטות נתעלם גם מהערך המדויק של כל פיקסל, ורק נחשוב עליו כעל "ריק" (נקודה) או "מלא" (סולמית).
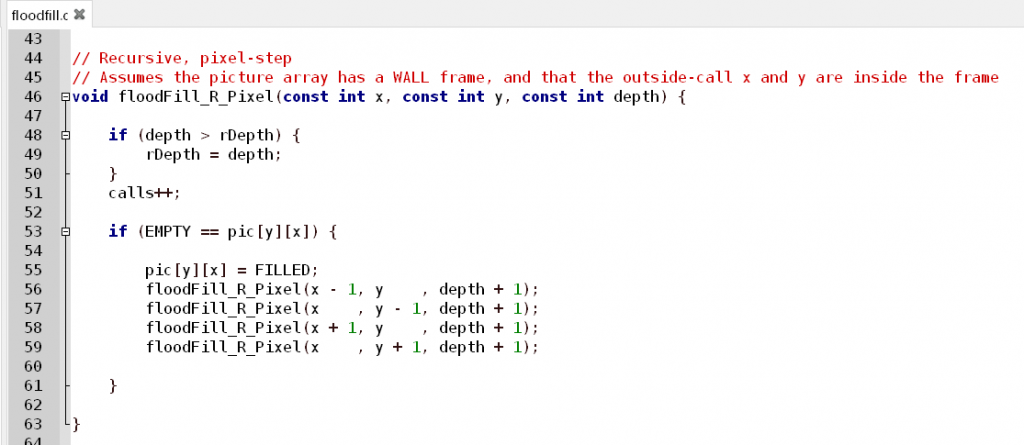
מערך של char בגודל הזה לא יתאים לארדואינו אונו – הוא תופס 2000 בייטים, וזה כל הזיכרון שיש לנו שם, לא יישאר מקום לשום דבר אחר. אבל אם נכווץ את המידע לביט או שניים לכל "פיקסל", אפשר יהיה להסתדר. בקוד שלי על ה-PC השתמשתי בכל זאת ב-char כדי לא להסתבך סתם. הנה קוד של פונקציית Flood Fill רקורסיבית נאיבית, שעובדת ברמת הפיקסל:
המשתנים rDepth ו-calls, והקבועים EMPTY ו-FILLED, מוגדרים איפשהו מחוץ לפונקציה כמובן. קראתי לפונקציה הזו עם קואורדינטות של אמצע התמונה פחות או יותר, ובסיום המילוי הסתבר שהפונקציה רצה 7177 פעמים, והגיעה לעומק של 1768 (!) שהיה מחסל בקלילות את ה-SRAM של לוח ארדואינו אונו. אפשר לחסוך המון קריאות אם מוסיפים בדיקה של ערך כל פיקסל לפני שקוראים לפונקציה עבורו: שינוי זה הקטין את מספר הקריאות הכולל ל-1794 בלבד – מה שמקצר משמעותית את זמן הריצה – אך העומק המרבי ירד רק ל-1767, וזה עדיין הרבה יותר מדי.
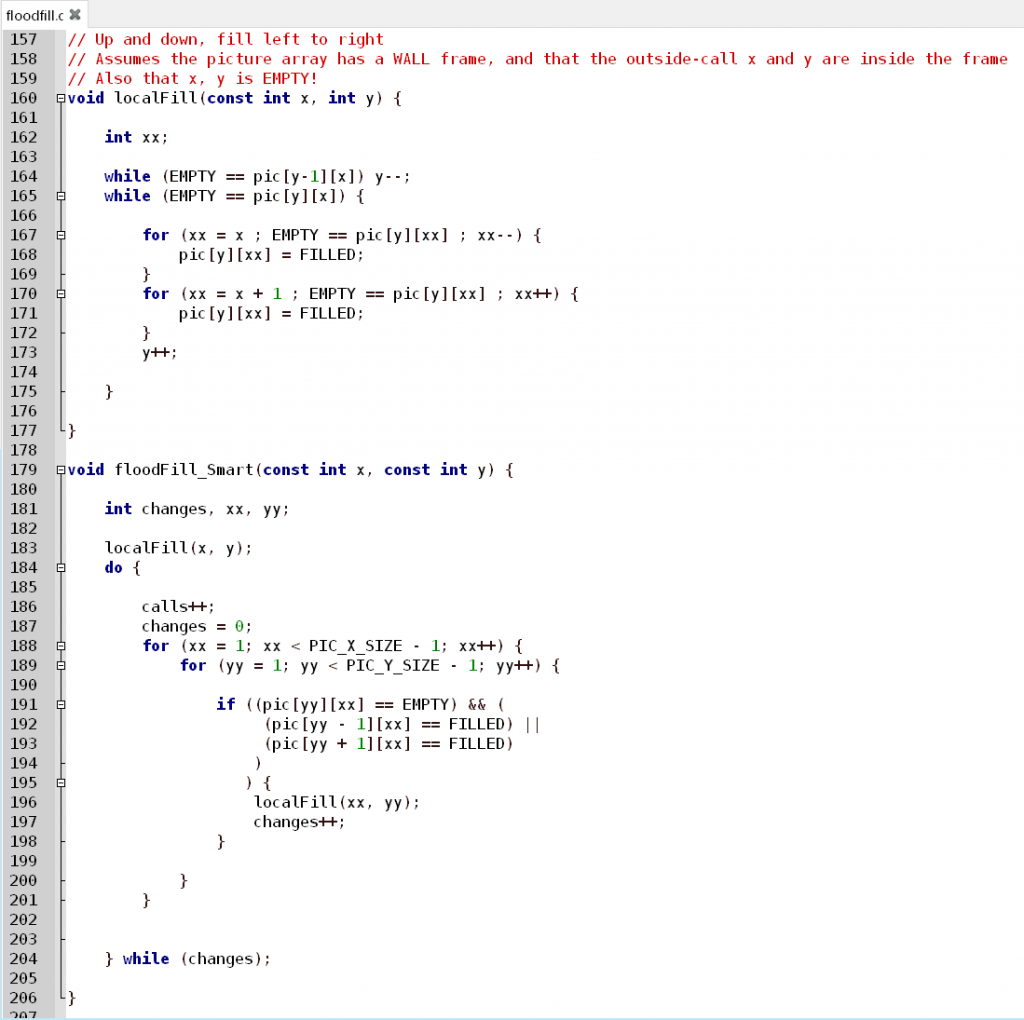
הפונקציה הבאה גם כן רקורסיבית, אך בכל סיבוב היא מנסה קודם כל למלא לבד את הפיקסלים הריקים מימין ומשמאל:
מבחינת עומק רקורסיה, לפחות, הפונקציה הזו הרבה יותר יעילה: המסגרת מולאה תוך 3589 קריאות (בלי אופטימיזציית קריאות כפי שעשיתי למעלה), ובעומק מקסימלי 13 בלבד. עם זה הארדואינו יוכל להתמודד… בהנחה שהשטח למילוי יהיה מלבן פשוט. מה יקרה אם נעבור לשטח מפותל ומורכב?
ללא אופטימיזציות, הפונקציה הרקורסיבית הנאיבית הייתה זקוקה ל-4281 קריאות ועומק מקסימלי 572, ואילו הרקורסיבית שממלאת לימין ולשמאל השלימה את המילוי ב-2141 קריאות, עומק מקסימלי 46. אם הייתי מתאמץ הייתי יכול "לתפור" מבוך במיוחד נגד הרקורסיה הזו, שיגדיל עוד יותר את העומק הדרוש. בהנחה שהתוכנית שלנו בארדואינו צריכה לאחסן את התמונה וגם להשאיר מקום לרקורסיות ולפעולות נוספות, המסקנה היא שהפתרון הרקורסיבי – ובהכללה, כל פתרון שמתבסס על הקצאה דינמית של זיכרון – עדיין מסוכן מדי. אבל איך אפשר לבצע Flood Fill אחרת?
אם אתם רוצים לחשוב על פתרון לבד, זה הזמן לעצור ולעשות זאת, כי מיד אציג את הפתרון שלי…
הפתרון שלי
המימוש של Flood Fill נוח כל כך ברקורסיה, כי בכל נקודה עשויים להופיע לנו מספר נתיבי התקדמות שונים [=פיקסלים סמוכים ריקים], שעלינו להיכנס לכל אחד מהם בתורו – ועדיין לזכור מאיפה באנו, כדי שנוכל להיכנס לאחר מכן לאלה שטרם היינו בהם. האם אפשר יהיה להשיג את אותה מטרה (לדעת איפה כבר היינו ולאן עוד צריך להמשיך) בנקודת זמן כלשהי שנבחר באקראי, פשוט מהסתכלות על פיקסלים בתמונה?
התשובה המיידית היא לא. נניח שאני מסתכל על פיקסל מסוים ורואה שהוא מלא. האם הוא חלק מפעולת המילוי הנוכחית וצריך להתקדם ממנו, או שהוא היה ככה בתמונה המקורית וצריך להתייחס אליו כאל מחסום בלבד? אי אפשר לדעת. אבל אם נוסיף "צבע ביניים", ערך פיקסל שאומר "אני לא אחד מהצבעים בתמונה, אני רק ממלא מקום זמני", כן אפשר יהיה לדעת. הסתכלו למשל על קטע התמונה הבא – נניח שזה איזשהו שלב ביניים שתפסנו באמצע תהליך המילוי, ושהתו ממלא-המקום הוא "/". האם יש ספק מה כבר מולא ומאיפה להמשיך?
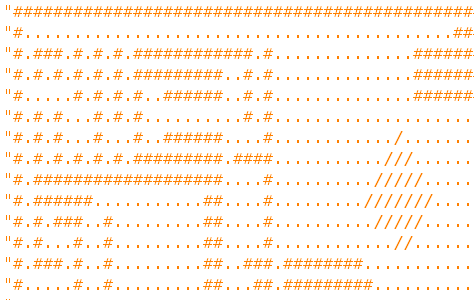
את התובנה הזו קל לתרגם לפונקציה נאיבית: אחרי שנסמן את הפיקסל הראשון בעזרת ממלא המקום, הפונקציה תעבור שוב ושוב בלולאה על כל התמונה, ותסמן כל פיקסל ריק שצמוד לפיקסל ממלא-מקום. אחרי מספיק איטרציות כאלה, כל הפיקסלים הרלוונטיים יהיו מסומנים, וכשנזהה שאין יותר פיקסלים לעדכן (=איטרציה שלא בוצע בה שום סימון), נוכל להחליף את ממלאי המקום בסימן הסופי הרצוי ולהשלים את הפעולה. שום רקורסיה, ועם חתימת זיכרון מינימלית ממש!
רק מה, זה יהיה איטי מאוד. כשהרצתי את הפונקציה הזו על השטח המורכב מקודם, נדרשו לה 72 מעברים – כל מעבר זה על כל הפיקסלים! – כדי להשלים את המילוי, ומעבר אחד נוסף דרוש כדי להמיר את ממלאי המקום לערך המילוי הסופי. זה אומר כמה מאות אלפי קריאות/כתיבות של פיקסלים, מה שייקח ה-מ-ו-ן זמן בתדר השעון של ארדואינו.
כפי שעשינו עם הפונקציה הרקורסיבית, גם כאן אפשר לבצע כל מיני אופטימיזציות, וגם האופי שלהן יהיה דומה. בין השאר, אפשר לסמן פיקסלים לכיוון ימין ולכיוון שמאל ברגע שמוצאים פיקסל חדש כלשהו לסימון – לא צריך לחכות לאיטרציות הבאות על התמונה כולה כדי להתרחב לצדדים. פעולה כזו חוסכת לנו גם את הצורך לבדוק שכנים מסומנים מהצדדים בפעם הבאה שניתקל בפיקסל ריק, כי אם היו לו שכנים רלוונטיים כאלה, הוא כבר היה מסומן…
הפונקציה הזו, שפיצלתי אותה לשתיים בשביל הקריאוּת, נזקקה לארבעה מעברים בלבד על השטח המורכב כדי למלא את כולו (לא כולל מעבר אחרון להמרת ממלאי המקום לצבע הסופי). גם כאן, ניתן למטב אותה עוד יותר, ומצד שני אפשר בתיאוריה ליצור שטח באופן שיאתגר ספציפית את צורת הפעולה של הפונקציה הזו ויכריח אותה לבצע הרבה יותר מעברים – אם כי שוב, העלות תתבטא רק בזמן הריצה, לא במשאבי זיכרון.
במקרים טיפוסיים, בכל אופן, גם מיקרו-בקר של ארדואינו יוכל לבצע כך Flood Fill בזמן סביר ובלי לסכן את מעט הזיכרון שיש לו.
עוד נקודה אחת: הזכרתי קודם שאפשר להגדיר תמונה עם ביט יחיד לכל פיקסל, אך שיטת המילוי הזו מחייבת לפחות שני ביטים לפיקסל, עבור התוספת של אופציית הצבע ממלא-המקום. במצב כזה, החיסכון שמושג על ידי הימנעות מרקורסיה מתקזז במידה מסוימת. עדיין, אנחנו לפחות יודעים מראש כמה זיכרון נדרש, ובמערכות אמבדד לעתים הוודאות חשובה לא פחות מהמספרים האבסולוטיים.
כל הקוד שהוצג למעלה נכתב לצורך הדגמה בלבד, ולא נבדק לעומק כך שאין שום אחריות. אם אתם רוצים לשחק איתו בכל זאת, תוכלו למצוא אותו כאן.