בתחילת שנות השמונים, ילדי ישראל השקיעו אינספור שעות בפתרון מבחנים אמריקניים על גבי צעצוע אלקטרוני שנקרא TOMY Teacher. באותם ימים, כידוע, כל בייט עלה הרבה כסף; אז איך הצליח המכשיר לזכור את כל הפתרונות של כל המבחנים?

המשחק

TOMY Teacher, או הגרסה האמריקנית Sears Quiz-A-Tron, מורכב משני אלמנטים: המכשיר עצמו (עם לחצנים, לדים מהבהבים ורמקול), ופנקסי מבחנים מודפסים על קרטון. המשתמש מניח פנקס בתוך המכשיר, בוחר את הדף שהוא רוצה לפתור, ומקיש את קוד הצבעים של המבחן – שמודפס בפינה השמאלית העליונה של הדף – כדי שהמכשיר יידע על איזה מבחן מדובר ומה התשובות הנכונות (לכל שאלה יש ארבע אפשרויות תשובה, ממוספרות 1-4). מי שענה נכון על כל עשר השאלות זכה לפידבק של הבהובים ומנגינה עליזה פרימיטיבית. כן, זה היה אחלה בילוי.

שמור או מחושב?

מכיוון שקוד הזיהוי של כל מבחן הוא תמיד באורך של שלוש יחידות, וכל יחידה יכולה להיות רק אחד מתוך שלושה צבעים (אדום, צהוב או כחול), מספר הקומבינציות האפשריות הוא 27 בלבד. לכל קומבינציה כזו יש עשר תשובות, שאם שומרים אותן בצורה חכמה, כל אחת מהן צריכה רק שני ביטים. עשו את החשבון ותגיעו ל-67.5 בייטים – לא כמות מטורפת, אפילו במונחים של 1980. כלומר, מבחינה טכנית לפחות, בהחלט ייתכן שיש בתוך המשחק ג'וק ROM עם טבלה צרובה-מראש של תשובות לכל אחד מ-27 המבחנים האפשריים.

אבל תחושת הבטן שלי היתה שהמידע הזה לא שמור בשום מקום אלא מחושב. למה? כי חישוב בזמן אמת – שיכול להיות פשוט מאד לביצוע – חוסך את ג'וק הזיכרון היקר (שוב, נכון ל-1980), מוזיל את עלויות הייצור ומגדיל את הרווחים. לא רציתי לפתוח בשלב זה את הצעצוע ולראות מה יש בפנים, כדי לא להרוס בטעות את המעגלים העתיקים. במקום זה, פתחתי את תוכנת האקסל במחשב…

החיפוש מתחיל

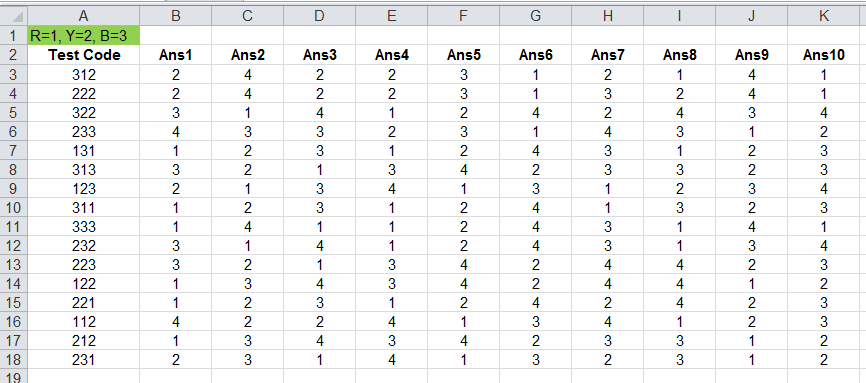
ראשית, נתתי מספר לכל צבע: 1 לאדום, 2 לצהוב ו-3 לכחול (על פי סדר הלחצנים שלהם במכשיר). לאחר מכן לקחתי שישה-עשר מבחנים עם קודים שונים, וכתבתי בגיליון אקסל את הקודים שלהם בשלוש ספרות (למשל 312 לכחול-אדום-צהוב) ואת כל התשובות הנכונות. כעת הגיע שלב הזן: להתבונן בריכוז במספרים ולקוות שתגיע ההארה.

קודים ותשובות של מבחנים. מה אתם מבינים מזה?

ואכן, מהר מאד הבחנתי בכמה רצפי תשובות שחזרו על עצמם. לדוגמה, במבחן 312 ובמבחן 222, שש התשובות הראשונות היו זהות לגמרי. זו היתה עדות חזקה לכך שמדובר בחישוב ולא בטבלה מוכנה מראש – כי מן הסתם, כל מתכנן סביר שממציא טבלה היה דואג שהתוצאות שלו ייראו יותר אקראיות, בלי רצפים שחוזרים על עצמם בצורה בולטת כל כך.

שיטת הזן לא קידמה אותי מעבר לתגלית הזו, אז פניתי לכיוונים מערביים יותר וניסיתי לחשוב איך מתכנן של מעגל אלקטרוני זול בשנת 1980 היה בוחר לייצר סדרות קבועות של מספרים כאילו-אקראיים. חישבתי את סכום הספרות של כל קוד מבחן, ואת השארית של חלוקת התוצאה ב-4. חישוב השארית נועד להתאים את הסקאלה של התוצאות לסקאלה של התשובות. לדוגמה, עבור מבחן 221, סכום הספרות הוא 5, והשארית מחלוקה ב-4 היא 1. בינגו! הסתבר שאם רק כותבים 4 בכל מקום שבו השארית יוצאת 0, החישוב הזה נותן תמיד את התשובה הנכונה לשאלה הראשונה!

תוספות

כעת היה ברור לי לגמרי שהתשובות מחושבות בזמן אמת, אבל הצלחתי למצוא רק את החוקיות של התשובה הראשונה. מה עם השאר? אחרי כמה השערות שלא קידמו אותי במיוחד, החלטתי להסתכל לא על התשובות הנכונות הגולמיות אלא על ההפרשים ביניהן. הרציונל כאן היה שאם התוצאה הראשונה היא סכום מצטבר של משהו, סביר להניח שגם הבאות הן סכומים מצטברים של משהו, וההפרשים יעזרו לי לראות מה מצטבר שם.

מיד כשיצרתי את עמודות ההפרשים התברר שצדקתי: תשובה 5 היתה תמיד גדולה באחד מתשובה 4 (כמובן, אחרי חישוב שארית), תשובה 6 היתה תמיד גדולה בשתיים מתשובה 5, ותשובה 10 גדולה באחד מתשובה 9.

שאר התשובות לא הראו דפוס אחיד שכזה. מה התווסף בהן? הרמז הבא הגיע כשהבחנתי, שבחלק מעמודות ההפרשים יש את כל המספרים (אפס עד שלוש כולל), אבל בחלק מהן המספר אפס לא הופיע. מאיפה מגיעים מספרים "אקראיים" בטווח 1-3 בלבד? אהה! ההפרש בין תשובה 2 לתשובה 1 היה תמיד הספרה האחרונה בקוד המבחן, ההפרש בין תשובה 7 לתשובה 6 היה הספרה האמצעית, וההפרש בין תשובה 9 לתשובה 8 היה הספרה הראשונה של הקוד!

נותרו לי שלוש עמודות הפרשים לא פתורות, אך מכיוון שכבר הבנתי את הראש של המתכננים זה לא לקח יותר מדי זמן. ההפרש בין תשובה 3 לתשובה 2 הוא סכום הספרות של הקוד (כן, אותו סכום שקבע את תשובה 1), ההפרש בין תשובה 4 ל-3 הוא מה שהתקבל בתשובה 2, וההפרש בין תשובה 8 ל-7 הוא תשובה 5.

לסיום, לקחתי שני מבחנים שלא הופיעו במדגם שלי, חישבתי את התשובות הצפויות ובדקתי אותן על המכשיר. ההתאמה היתה מושלמת.

החומרה

השאלה היחידה שנותרה היא איך העסק הזה מומש באלקטרוניקה של המשחק. המנגינות ודפוסי ההבהוב של המשחק מעידים, לדעתי, על נוכחותו של מעבד כלשהו, ולא רק רכיבים לוגיים פשוטים. אם זה נכון, סביר להניח שהוא משתתף איכשהו בחישוב הנ"ל, אף על פי שניתן עקרונית לבצע את החישוב גם עם רכיבים כמו Adders, Counters או Shift registers.

בינתיים לא הצלחתי למצוא ברשת מידע על המעגלים שבתוך ה-TOMY Teacher, וכאמור, כל עוד המכשיר שאצלי עובד והילדים משחקים בו, אני לא מעוניין להתעסק איתו יותר מדי. הסקרנות תצטרך לחכות…

עדכון: בפוסט ההמשך כאן ניתחתי קצת את רכיבי החומרה של המשחק, וגיליתי את המבחנים הסודיים שאיש לא ראה מעולם…