כמה זמן לוקח למיקרו-בקר להכפיל שני מספרים? מסתבר שאפילו לשאלה פשוטה כל כך, התשובה אינה פשוטה – והיא מדגישה את הירידה לפרטים ואת צורת החשיבה הדרושות כדי להשיג מקסימום ביצועים במערכות Embedded.
לפני כחצי שנה כתבתי פוסט על העלות הגבוהה של פעולות חילוק במיקרו-בקרים, ושם התייחסתי לפעולת הכפל כזולה יותר, מבלי לפרט. כעת הגיע הזמן לצלול לעומק ולברר כמה עולה לנו כל הכפלה. המוטיבציה לפוסט הזה היא תגובה שקיבלתי לפוסט הקודם, על טבלת ה-lookup, שבה נשאלתי למה טרחתי ליצור טבלת ערכים כשאפשר לחשב אותם בזמן אמת בפעולת כפל בסיסית.
ראשית, איך בעצם מתבצעת במיקרו-בקר פעולה של כפל? איך מתבצעת בכלל הכפלה? בבית הספר היסודי למדנו שכפל הוא פשוט שם אחר להרבה חיבורים: למשל, התרגיל 4*5 הוא שווה ערך לתרגיל 5+5+5+5 (או 4+4+4+4+4). אם יש לנו חומרה שמסוגלת לבצע פעולת חיבור ולהריץ לולאות פשוטות, אנו יכולים לממש כפל בצורה הזו. אלא שכמובן, זה יהיה מימוש מאד לא יעיל, במיוחד במספרים גדולים: הכפלה של מאה במאה תצריך תשעים ותשע פעולות חיבור, וזה עוד לפני שדיברנו על הלולאה שבתוכה הן צריכות להתבצע.
לשמחתנו, יש כמה טריקים שאנחנו יכולים לעשות כדי לזרז את התהליך. אחד מהם, שאת שורשיו אפשר למצוא במצרים העתיקה (בחיי!), מנצל את התכונות השימושיות של ייצוג מספרים בבסיס בינארי. בואו נסתכל על המספר 5 בייצוג בינארי:
101
המיקום הימני ביותר במספר – לא הביט אלא המיקום שלו! – שווה 1, וכל מיקום אחר שווה פי שניים מהמיקום שמימין לו. נסתכל על הביטים שערכם "1" במספר ונסכם את שווי המיקומים שלהם: 1 + 4, שזה כמובן 5.
אנחנו רוצים להכפיל את המספר הזה ב-4, אז כל מה שצריך לעשות זה לשנות את השווי של המיקום הימני ביותר מ-1 ל-4. השווי של המיקומים האחרים מחושב לפי הכלל הקודם – הכפלה פי שניים בכל צעד שמאלה. כעת, שווי המיקומים של הביטים שערכם "1" הוא 4 ועוד 16, שזו התשובה הנכונה. ההכפלות שאנחנו עושים בתהליך הזה הן תמיד פי 2, שזה פשוט להוסיף את המספר לעצמו פעם אחת, וכך אנחנו פותרים את התרגיל בפעולות חיבור בלבד.
בשיטה הזו, בהנחה שאנחנו לא עושים שום אופטימיזציות, מתעלמים ממספרים שליליים ולא "גולשים" לטיפוסי משתנים עם מספר ביטים שונה, הכפלה של שני מספרים כלשהם בני 8 ביטים מיתרגמת למשהו כמו 16 פעולות השמה או חיבור בסיסיות, בתוספת מספר דומה של פעולות לניהול הלולאה שעוברת על הביטים. הרבה פחות ממאות הפעולות שהיינו צריכים בשיטה הקודמת – ועדיין, הרבה יותר מאשר פעולה אחת בשפת אסמבלי. אם המיקרו-בקר שלנו מבצע כפל בצורה כזו (וזה אכן המצב בחלק מהמקרים), העלות של כפל היא הרבה יותר גדולה מאשר, נניח, חיפוש בטבלת lookup.
האם פעולת כפל חייבת תמיד להתבצע כאלגוריתם בתוכנה? התשובה שלילית. את האלגוריתם שהוצג למעלה, למשל, אפשר "לנסח מחדש" ברמה של שערים לוגיים, בחומרת המיקרו-בקר, ואז ההכפלה תתבצע תוך שני מחזורי שעון או אפילו אחד. העניין הוא שזה מצריך הרבה טרנזיסטורים, ובמיקרו-בקרים קטנים או בארכיטקטורות ישנות המתכננים לא מצאו לנכון להשקיע את המאמץ. במשפחת ATmega, למשל, זה קיים, אבל ב-ATtiny לא, ויכולות להיות להבדל הזה השלכות משמעותיות מאד.
איך יודעים אם למיקרו-בקר מסוים יש פעולת כפל בחומרה או לא? ראשית, מכיוון שזה פיצ'ר שימושי כל-כך, הוא יודגש במקום בולט ב-datasheet:
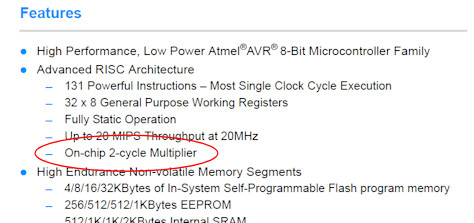
בנוסף, אפשר ללכת לפירוט ה-Instruction Set של המיקרו-בקר (פקודות האסמבלי שהוא מכיר), ולחפש שם פקודה עם השם המקובל MUL. יש? הרווחתם. אין? תכנתו בזהירות…
