שאלה עם פתרון רקורסיבי טריוויאלי, לכאורה, הופכת לפחות-טריוויאלית כשכופים על הפתרון גם מגבלת זמן, ומהווה דוגמה מצוינת לעיקרון של תכנות דינמי.
השאלה, שהופיעה באתר codechef ונחשבת ברמת מתחילים, היא זו (בניסוח-מחדש משלי): נתון "משולש" עשוי מ-N מערכים של מספרים, כך שבמערך העליון יש מספר אחד בלבד, במערך שמתחתיו שני מספרים, בשלישי שלושה וכן הלאה. "נתיב" במשולש הזה הוא מעבר בין תאים במערכים מלמעלה עד למטה, כאשר בכל שלב אפשר או להישאר באותו אינדקס במערך, או להתקדם אינדקס אחד בלבד. מבין כל הנתיבים האפשריים, מהו הסכום המקסימלי של נתיב במשולש?
הנה ארבעה עותקים של משולש לדוגמה, שבו N=3, ועל כל עותק מסומן בצהוב נתיב שונה. יש בסך הכול ארבעה נתיבים אפשריים (תת-חידה: כמה נתיבים אפשריים יש במשולש כלשהו, כפונקציה של N?)
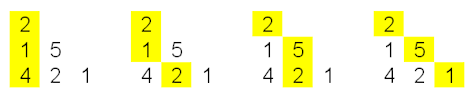
סכום המספרים בנתיב השמאלי באיור הוא 7 (כי 2+1+4), בנתיב השני משמאל זה 5, ובנתיב השלישי משמאל מתקבל הסכום הגדול ביותר מבין כל הנתיבים – 9. איך נכתוב תוכנית שמוצאת את הנתיב עם הסכום המקסימלי?
מתכנת חסר כל ניסיון עשוי לחשוב שאפשר לפתור זאת במעבר יחיד: להתחיל למעלה, ובכל צעד, פשוט לבדוק איזו מהאפשרויות (להישאר באותו אינדקס או להתקדם) מוסיפה יותר לסכום. זו טעות, כפי שמודגם במשולש באיור למטה. במערך השני נעבור לאינדקס השני, כי 2 גדול מ-1, אבל אז במערך הבא לא נוכל לחזור ל-8, שגדול יותר מכל המספרים האחרים גם יחד.

גם חיפוש "מהסוף", שיתחיל מהמספר הכי גדול במערך התחתון, יכול להיכשל מסיבה דומה. כך או אחרת, פתרון אמיתי יצטרך לעבור על כל הנתיבים האפשריים. למתכנתים טיפה יותר מנוסים, המשפט הזה אומר רקורסיה: עבור כל מספר, אני בודק את שתי האפשרויות מתחתיו, על ידי כך שעבור כל אפשרות אני בודק את שתי האפשרויות שמתחתיה, על ידי כך שעבור כל אפשרות… עד שמגיעים למערך התחתון, ואז אפשר להסתכל על הסכום שהצטבר לאורך הדרך ולבחור את המנצח.
אם לא נתבלבל בקוד, הפתרון הרקורסיבי יעבוד. אבל הוא ייקח הרבה זמן. מי שפתר את תת-החידה קודם יודע שבמשולש בגודל N יש 2N-1 נתיבים אפשריים, ואם N הוא מספר גדול (יחסית!) כמו 40 או 50, זה אומר טריליונים על גבי טריליונים של נתיבים. גם מחשב מודרני מהיר יזדקק לימים רבים כדי לפתור את הבעיה, ובמיוחד אם כותבים את הקוד בשפה עצלה כמו פייתון.
הסוד לפתרון מהיר של החידה טמון בכך שהרקורסיה מבצעת המון פעולות מיותרות. הסתכלו למשל על המשולש באיור הבא, וליתר דיוק על המספר 3 שנמצא באמצע השורה השלישית. אנחנו יכולים להגיע אליו בשתי דרכים שונות: דרך 2 ו-1 או דרך 2 ו-5. הרקורסיה הפשוטה אכן תגיע אליו פעמיים, ובכל פעם תחשב מחדש את כל האפשרויות להמשך הנתיב. דמיינו שיש עוד 40 שורות למטה במקום רק אחת, ותבינו כמה עבודה מיותרת הרקורסיה עושה כאן.
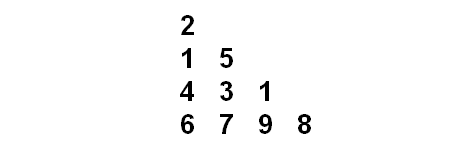
מה שאנחנו צריכים הוא "זיכרון". בפעם הראשונה שהגענו למספר מסוים, אנחנו עוד לא יודעים מה הסכום המקסימלי שניתן להפיק ממנו והלאה, וצריך לחשב את זה. אבל אחרי שחישבנו פעם אחת, למה שלא נשמור את התוצאה איפשהו בצד, כדי שבפעם הבאה שנגיע למספר הזה התוצאה כבר תהיה נתונה לנו? זה, בגדול, הרעיון של תכנות דינמי.
אבל איך עושים את החישוב? הרי ראינו שכדי לחשב את הנתיב המיטבי מלמעלה למטה צריך לעבור ברקורסיה על כל האפשרויות… אז בואו נסתכל על זה הפוך. נתחיל מלמטה, מתת-הנתיבים הקטנים ביותר שצריך לחשב, כלומר מהשורה האחת-לפני-אחרונה. באיור למעלה, מהספרה 4 אפשר להתקדם ל-6 או ל-7. אנחנו יודעים ש-7 עדיף, וש-4 ועוד 7 זה 11, אז במקום ה-4 נכתוב 11. מה אכפת לנו "לדרוס" את ה-4? הרי לא נצטרך לעשות את החישוב הזה שוב. באותו אופן, במקום ה-3 נכתוב 12, ובמקום ה-1 נכתוב 10. שימו לב שלא קבענו מי מהמספרים האלה עדיף עבור התשובה הסופית, כי אנחנו עוד לא יודעים מה יש מעליהם. פשוט חסכנו את כל החישובים החוזרים על השורה התחתונה, ואנחנו לא צריכים לגעת בה יותר לעולם.
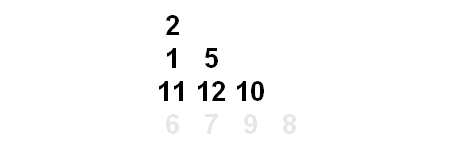
כעת נעלה שורה אחת למעלה ונחפש את הבחירה האופטימלית (והסכום) עבור שני המספרים שבה, 1 ו-5. באותה שיטה כמו קודם, נחליף את 1 ב-13, ואת 5 ב-17. לסיום נעבור לשורה הראשונה ונראה שהסכום המקסימלי מבין הנתיבים האפשריים במשולש כולו הוא 19. אם היו שואלים אותנו לגבי צורת הנתיב עצמו היינו קצת בבעיה, אם כי אפשר כמובן למצוא פתרונות "דינמיים" גם לזה. נפטרנו מהרקורסיה הממושכת (ומרקורסיה בכלל) ופתרנו את החידה בזמן ריצה קצר מאוד.
לא כל תוצאה שמחשבים מראש ומאחסנים לשימוש מאוחר יותר היא תכנות דינמי: ההגדרה ה"רשמית" של הטכניקה מתייחסת ספציפית לפעולות שהיינו מבצעים ברקורסיה, כאשר הרקורסיה הזו סורקת את אותם תת-פתרונות שוב ושוב. אחרת זה פשוט לולאה, או טבלת חיפוש.

פתרון יפה מאוד, לא יודע כמה הייתי חושב עליו בעצמי.