בפוסט הקודם טיפלנו במקרה הקל, שבו האמן צריך היה לשלם על כל CJ וכל JC שמופיעים בציור שלו. כעת אנחנו עוברים לשלב הבונוס של אותה חידה, שבו שני הצירופים האלה – או רק אחד מהם! – יכולים להוות מקור הכנסה לאמן.
אם לא קראתם את הפוסט הקודם, עשו זאת עכשיו, כי אני לא אסביר את כל החידה מחדש ואתם לא תבינו כלום…
אם כן, ראינו שכאשר הצירופים JC ו-CJ עולים שניהם כסף, ומכיוון ששניהם מייצגים שינויים (לעומת הצירופים CC ו-JJ שאין בהם שינוי), האסטרטגיה האופטימלית היא לא להוסיף שום שינוי מעבר למה שנכפה עלינו במחרוזת הקלט. למעשה, אפילו לא צריך למלא בפועל את האזורים ה"ריקים" במחרוזת אלא פשוט לזהות את השינויים הקיימים בה, אם יש כאלה, ולסכום את ערכיהם. זה אלגנטי וקל למימוש, במיוחד בפייתון.
כשהעלות של שני הצירופים האלה יכולה להיות שלילית (כלומר, להכניס לאמן כסף), כל צורת החשיבה צריכה להשתנות. זה לא רק ששינויים נעשים רווחיים וכדאי ליצור מקסימום שינויים: יכול להיות גם ששינוי אחד יהיה יותר רווחי מהשני, וזה ישפיע על קבלת ההחלטות של האלגוריתם. לדוגמה, אם מקבלים את המחרוזת "??", יהיה הבדל בתוצאה אם נמלא אותה כ"JC" או כ"CJ", ואם נקבל את המחרוזת "??C" ייתכן שנבחר תשובה אחרת לגמרי עבור אותם שני סימני שאלה בהתחלה. ולא לשכוח, ייתכן גם מקרה שבו לצירוף אחד תהיה עלות חיובית ולשני שלילית. איך ניגשים לזה?

שום פתרון לא קפץ לי לראש, אז התחלתי לחשוב על דוגמאות ספציפיות. נתחיל במחרוזות עם שני סמלים בלבד. אם שניהם מאוכלסים (C או J), פשוט בודקים מה הערך של הצירוף. אם אחד מהם או שניהם סימני שאלה, כך או אחרת חייבים לבדוק את כל האפשרויות לאכלס אותו/אותם.
מה קורה כשיש שלושה סמלים במחרוזת? ניתן כמובן לבדוק גם פה את כל האפשרויות, אבל שוב, זה אלגוריתם מאוד בזבזני שיהפוך ללא-מעשי בהמשך. במקום לברוח אליו, בואו נחשוב במושגים מופשטים יותר של שינוי. נניח ששני הסמלים בתחילת ובסוף המחרוזת הזו מאוכלסים ושונים זה מזה, ובאמצע יש סימן שאלה. למשל "C?J". מה שלא אשים באמצע, יהיה במחרוזת הסופית רק שינוי אחד ויחיד, מ-C ל-J. לעומת זאת, מה יקרה אם הסמלים בהתחלה ובסוף יהיו זהים, למשל "C?C"? אם אשים באמצע C לא יהיה שום שינוי, אבל אם אשים J, במחרוזת הסופית יהיו בהכרח שני שינויים, בכיוונים הפוכים. ובניסוח עוד יותר כללי, אם הסמלים בהתחלה ובסוף זהים, אז לכל שינוי שאבצע אי-שם באמצע חייב בהכרח להתקיים שינוי נוסף בכיוון ההפוך!
נישאר רגע במקרים שבהם שני הסמלים הקיצוניים זהים, וביניהם יש רק סימני שאלה. לא משנה מה אורך המחרוזת, לפי הכלל שניסחתי בסוף הפסקה הקודמת, מספר השינויים חייב להיות זוגי (אני כולל בזה את 0), נכון? וכל זוג שינויים כזה הוא בהכרח בכיוונים הפוכים, נכון? ואני יודע מה העלות/רווח של כל כיוון של שינוי, אז אני יכול לחבר את הסכומים ולראות אם ישתלם לי להכניס למחרוזת שינויים או לא. כדי לדעת את הסכום הסופי המדויק, אצטרך לדעת גם כמה זוגות שינויים נכנסים ברצף של X סימני שאלה. כבר ראינו שכאשר X=1, מספר זוגות השינויים יכול להיות אפס או אחד. קחו נייר ועפרון ותראו שכאשר X=2, מספר זוגות השינויים עדיין יכול להיות רק אפס או אחד. כש-X=3, אפשר להגיע לשני זוגות שינויים ("CJCJC"). בהכללה, כל סימן שאלה אי-זוגי נוסף מוסיף לנו אופציה לזוג שינויים.
נעבור למקרים שבהם הסמלים בהתחלה ובסוף מאוכלסים, אבל שונים זה מזה. הם כופים עלינו מראש שינוי אחד בלתי נמנע. מעבר לזה, סימן שאלה אחד בלבד ביניהם לא ישנה כלום, שני סימני שאלה יתנו לנו אופציה לזוג שינויים בכיוונים הפוכים, ובהכללה, כל סימן שאלה זוגי מוסיף לנו אופציה לזוג שינויים.
ובהכללה עוד יותר הכללתית, בכל רצף סימני שאלה בין שני סמלים, אנחנו יכולים להוסיף למצב הקיים רק זוגות שינויים בכיוונים הפוכים. אם סכום העלויות של שני כיווני השינוי חיובי (לרעת האמן) או אפס, אין טעם להוסיף כלום, ואם הסכום שלילי, רצוי להוסיף כמה שינויים שרק אפשר. מבחינת כדאיות כלכלית, זה הכול או כלום. ומה קורה אם אחד מהסמלים הקיצוניים, או שניהם, סימן שאלה? אז נוכל לשים במקומם מה שיותר משתלם לנו, כמובן.
כל המצבים שהזכרתי עד כה דיברו על רצף של סימני שאלה באמצע. יכול בהחלט להיות שגם באמצע מחרוזת יהיו סימנים מאוכלסים, אבל זה לא מפריע: אפשר פשוט לחתוך אותה לתת-מחרוזות מתאימות ולבצע את החישובים עליהן.
כל הניתוח שכתבתי למעלה היה מהראש בלבד. זה נראה לי הגיוני, אבל זה לא אומר שזה נכון. הגיע הזמן לכתוב קוד ולבדוק. התחלתי בגרסת פייתון, והבעיה היא שבאתר התרגול של Google Code Jam הפידבק מינימליסטי ולא ממש עוזר בדיבוג. אז עשיתי הרבה טעויות קטנות וטפשיות בדרך, אבל כולן היו במימוש הטכני – הרעיון עצמו היה בסדר, ולהוכחה, הקוד עבד בסופו של דבר.
רק אחרי שהצלחתי, ניגשתי לדף ה-Analysis של הבעיה, שבו מוסברת דרך הפיתרון. להפתעתי, הדרך שהם הציעו מסתמכת על תכנות דינמי ורקורסיה (שתהיה, אם הבנתי נכון, עמוקה הרבה יותר מזו שבקוד שלי). שמחתי מאוד לראות שהכיוון שלי היה מקורי יחסית, וככל הנראה צורך פחות משאבים ויכול, בשפת התכנות הנכונה, לרוץ אפילו על מיקרו-בקר פשוט 🙂
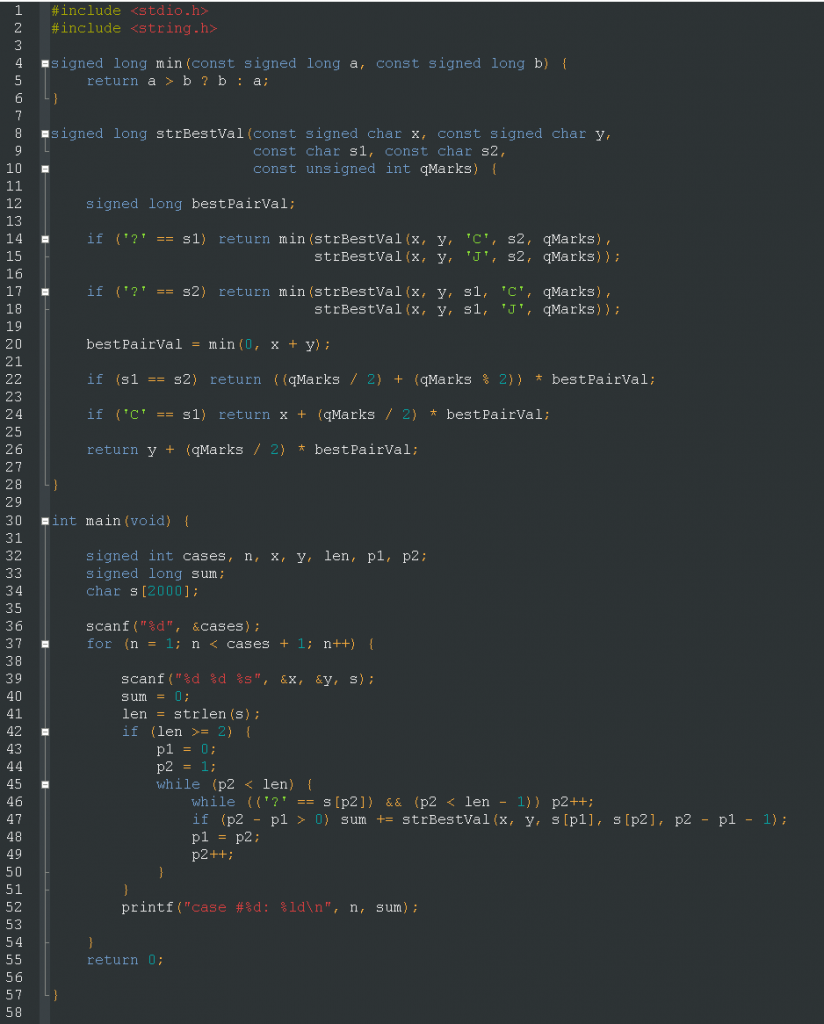
הדבר היחיד שנשאר, בשביל התרגול בלבד, הוא לכתוב קוד מקביל בשפת C. כיוון שלמדתי מהניסיון של גרסת הפייתון, הייתה לי כאן טעות אחת בלבד – ב-printf הסופי של התוצאה השארתי את הפורמט %lu מהחידה הקודמת, שהוא כמובן מיועד למספרים unsigned, בזמן שהתשובה כאן יכולה בהחלט להיות שלילית. אחרי שהחלפתי אותו ל-%ld הכול הסתדר ושאלת הבונוס נפתרה בשיטה שלי גם ב-C: