בכל ההתייחסויות הקודמות פה בבלוג למחלקי מתח, או שהשתמשתי בשני נגדים קבועים, או – אם אחד מהם היה נגד משתנה כלשהו – בחרתי לנגד השני ערך "מתאים" בלי להסביר בדיוק איך ולמה. הגיע הזמן להתייחס לנקודה הקטנה והחשובה של בחירת ערך נגד אופטימלי.
למי שעוד לא סגור על התיאוריה של מחלק המתח הבסיסי, הנה פוסט מפורט. בעיקרון, אנחנו בוחרים ערכים לשני נגדים כדי ליצור יחס מסוים ביניהם, כאשר באופן כללי מומלץ להימנע מערכים קטנים מדי (=בזבוז זרם) או גדולים במידה קיצונית (=הפרעות פוטנציאליות מקיבוליות זעירה במעגל).
אבל כשאחד הנגדים הוא דינמי, איזשהו חיישן שמגיב בשינוי משמעותי של ההתנגדות לפרמטרים סביבתיים כמו אור, חום* או לחץ, המשימה שלנו הופכת לאחרת: לא למצוא לנגד השני ערך שיפיק במוצא מתח ספציפי, אלא ערך שייתן טווח מתחים מקסימלי.
מה זאת אומרת? נניח שיש לנו נגד תלוי-אור (LDR), שטווח ההתנגדות שלו הוא אלף אוהם בתאורה מקסימלית עד מאה אלף אוהם בחושך מוחלט. נניח גם שמצאנו במגירה נגד רגיל של 1 מגה-אוהם, והחלטנו לשלב אותו עם ה-LDR במחלק מתח. הנגד הרגיל הזה יהיה בתפקיד R2, שמחובר מצד אחד לנקודת המוצא ומצדו השני לאדמה. מתח ההפעלה של המעגל כולו יהיה 5V.
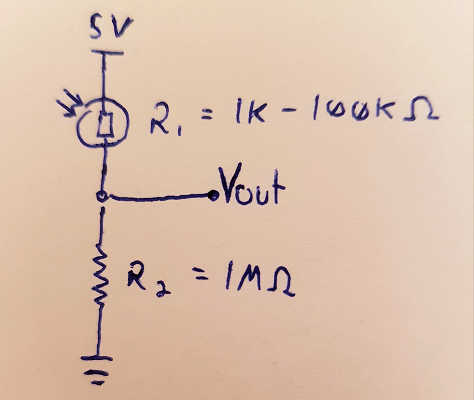
לפי הנוסחה של מחלק המתח והנתונים הנ"ל, בתאורה מקסימלית, מתח המוצא יהיה 4.995V. בחושך מוחלט, מתח המוצא יהיה 4.545V. במילים אחרות, ההפרש בין מתחי המוצא בשני המצבים הקיצוניים האלה יהיה 0.45V בלבד. אם נבצע קריאה אנלוגית של המתח בעזרת פין קלט של ארדואינו, למשל, אנחנו למעשה "נבזבז" את רוב טווח המתחים שהוא מסוגל לזהות.
נניח כעת שבמקום נגד של 1 מגה-אוהם מצאנו נגד של 50 קילו-אוהם. מתחי המוצא במצבים הקיצוניים יהיו כעת 4.902V ו-1.667V, הפרש של 3.235V – גדול פי שבעה מההפרש שקיבלנו עם הנגד הגדול! וכמובן, ככל שההפרש הזה יהיה גדול יותר, כך נוכל לקרוא את הפלט ברזולוציה גבוהה יותר עם ה-ADC שלנו, וזה כמעט תמיד מה שאנחנו רוצים.
השאלה כעת היא מהו הערך האופטימלי של נגד R2, זה שיעניק לנו – בהינתן ערכי הקיצון הידועים של R1 המשתנה – את טווח התוצאות הגדול ביותר. בעצם, יש לנו פונקציה מתמטית די בסיסית, ואנחנו מחפשים את ערך R2 שייתן לנו את התוצאה המקסימלית.
הפונקציה אולי בסיסית, אבל לצערי הידע שלי במתמטיקה עוד יותר בסיסי, ולא הצלחתי לחשוב בקלות על דרך לפתרון. מה שכן יכולתי לעשות בקלות זה לכתוב תוכנה שמוצאת פתרון (ליתר דיוק, הערך השלם הקרוב ביותר לפתרון) בהינתן מינימום ומקסימום של R1.
ידעתי אינטואיטיבית שהפתרון חייב להיות איפשהו בין שני הערכים האלה, והתוכנה אישרה את האינטואיציה. אבל התשובה היא לא בדיוק אמצע. היא קרובה יותר לערך הנמוך, ואחרי חיפוש באינטרנט הגעתי למסמך הזה, שמפרט פתרון מתמטי של אותה בעיה, רק בהיפוך התפקידים של R1 ו-R2. אם לא בא לכם לקרוא שם, השורה התחתונה היא שהערך האופטימלי הוא הממוצע הגאומטרי של שני ערכי הקיצון, כלומר שורש המכפלה של שני הערכים. השורש של אלף-כפול-מאה-אלף הוא עשרת אלפים. נגד 10K ייתן לנו מתחי קיצון של 4.545 ו-0.454 לערך, כלומר טווח של 4.091 וולט. אתם מוזמנים לבדוק ולראות שזה אכן הטווח המרבי.

אז בכל פעם שמודדים משהו בעזרת חיישן "התנגדותי" במחלק מתח, זו השיטה למצוא את ערך הנגד השני שימקסם את טווח הפלט. פשוט וקל. מה שכדאי לזכור, לפני שרצים לנוסחה, זה שלפעמים טווח ההתנגדות התיאורטי של החיישן הוא לא הטווח הרלוונטי ליישום הספציפי. לדוגמה, אם LDR מסוים יורד עד 1K אוהם באור שמש מלא אבל הפרויקט יישב תמיד בתוך מחסן נטול חלונות, כדאי לבדוק מה טווח ההתנגדות שלו בתנאי אמת, בשטח, ולבצע את החישוב לפיו. הרזולוציה שנוכל להשיג כך תהיה הרבה יותר גבוהה.
* זה המקום להיזכר באמירה נהדרת של Elecia White: "כל החיישנים הם חיישני טמפרטורה, חלקם מודדים גם דברים אחרים."

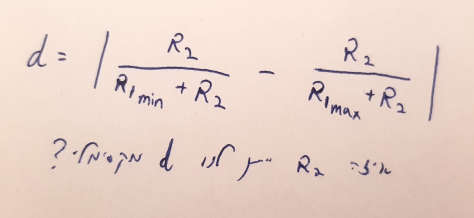
היי רציתי לדעת למה התייחסת לערך המינימלי של הldr באור כ-1000 אום? ראיתי שההתנגדות שלו באור בדרכ היא סביבות ה200. תודה
בעיקר כי 1000 זה מספר עגול ונוח לחישובים 🙂 זה די קרוב לערכים שראיתי בפועל, אבל כמובן יש כל מיני LDR עם תגובות שונות, במיוחד הדגמים הסיניים הזולים, אז חשוב באמת לבדוק את הרכיב בשטח ולא לסמוך בצורה עיוורת על פוסטים ברשת.
תודה. אז בעצם הנגד של 10K שראיתי שכולם משתמשים בו באינטרנט זה פשוט כי זה נוח וההתנגדות שלו שווה או גדולה ממה שצריך?
בכל מקרה נגדים תלויי אור נותנים טווח רחב של התנגדויות (בהתאם לתנאי התאורה כמובן), לא מספר אחד ספציפי.
באופן עוד יותר כללי, יש מעגלים שבהם ערך נגד מדויק הוא כמעט חסר משמעות, ויש מעגלים שבהם הוא חייב להיות מדויק עד עשירית האחוז ואפילו יותר – הכול תלוי בתפקיד של הנגד במעגל ובתפקיד של המעגל עצמו.
תודה עידו! מעניין כתמיד..
כשקראתי קפץ לי לראש מקרה נוסף בו משתמשים בממוצע גיאומטרי- מציאת התדר המרכזי בין שני תדרי מחצית ההספק במסנן מעביר פס.
לכן מאוד אהבתי את הדוגמא "המוזיקלית" במסמך שצירפת..
רעיון אופציונלי לפוסט המשך בנושא, שיפור מחלק המתח הבסיסי, ושימוש בגשר ויטסטון לדוגמא יכול להעניק ערך מוסף.
אם הייתי יודע מה זה תדר מחצית ההספק… 🙂
פשוט מאוד!
מסנן הוא מעגל שתפקידו להעביר רק חלק מתדרי המבוא למוצא.
נגיד ואנחנו מכניסים למסנן מעביר פס (Band pass filter) מתח חילופין בעוצמה כלשהי אך תדירותו משתנה, ומשרטטים גרף של היחס בין המוצא לכניסה כתלות בתדר- תתקבל עקומת פעמון.
במרכז הפעמון יתקבל ההספק המקסימלי במוצא, זהו התדר המרכזי הנ"ל.
משני צידי התדר המרכזי ישנם שני תדרים אשר נקראים תדרי מחצית ההספק, כשמם כן הם- תדרים בהם מתקבל חצי מההספק המקסימלי במוצא.
כל תחום התדרים הנמצא בין תדרי מחצית ההספק נקרא רוחב הפס (Band width) זהו התחום אותו המסנן "מעביר", את כל שאר התדרים הוא "מסנן" החוצה..
הבנתי. וזה אומר שהפעמון מוטה לצד מסוים (אחרת הממוצע היה חשבוני, לא גאומטרי)? ומה האלמנט הלא-לינארי בפילטר שגורם לזה? התגובה של קבלים בתדרים שונים?
מסיבות כאלה ואחרות בד"כ מציגים את הגרף על ציר תדר לוגריתמי (מכפלה קבועה בין השנתות בניגוד להפרש קבוע) ואז הפעמון נראה סימטרי.
אבל אתה צודק בהחלט, במידה ונשתמש בציר ליניארי תובחן נטיה לאחד הצדדים.
וזה אכן נגרם מכך שחלק מרכיבי המסנן (קבלים/סלילים) תלויים בתדר (בניגוד לנגדים 😜) וכן מאופן חיבורם במעגל בטור/במקביל/שילוב כלשהו..
לקריאה נוספת בנושא ניתן לחפש bode plot .
הנאה מובטחת 😎